
from Todd Spencer <lildog@inreach.com>: I decided to start my designing with a model of a futuristic tank from a video game, I thought it would be a snap to design because there are no curves, just straight lines and angles. Here is where my question arises. I am doing real well I think, my pieces fit and line up right. But it has been through much trial and error. Many scratch builds and rebuilds.Anyhow, I realize it does take many test fits to design but I am looking for some "equations". Think of a pyramid. A relatively simple design. Say I wanted a pyramid so high and so wide at the base. How do you determine the length of the side with those variables. Now before you say just measure from the top to bottom, if you look at it(or imagine it) the sides are angled in two directions, out and towards you. Follow me? Which makes the longer in those directions. I hope this is clear. How do you determine the length?
from Bob Santos <SantMin@aol.com>: I guess I'm a dummy, but I don't see what all this "math" is about !Here's an example of a graphical solution for the pyramid. Note how the triangle is redrawn at its true height.My background is in mechanical drawing and if you can draw a side and top view of your pyramid (in actual size or any scale), you're done, you can measure any side or diagonal you need. In fact, add a pair of dividers and you can draw the pattern to cut out to fold up into your pyramid without measuring anything.
from Will Hartung <vfr750@netcom.com>: Okay all, here comes the nitty gritty for Todd.But first, a couple of notes.
This is best viewed using a fixed width font. Courier and Monaco are common.
Bob Santos - It does not surprise me at all that there are techniques and methods to do what Todd is trying to do using technical drawing tools. Paper Models have been around since...well...paper, I guess, anyway, since long before computers, calculators, slide rules etc. may have been considered tools of the trade. However, when I had my opportunity to take technical drawing, I somehow ended up in the school band instead, so most of these techniques are completely unknown to me. Of course, anything but the most basic tenets of music are lost to me as well. I didn't do well in band. I can barely play a radio.
I am rather computer centric, so I look at most anything as a 'computer problem'. So.
To all of the folks helping Todd out with the Pyramid Formula, I think that he is looking for something a LOT more general than a simple pyramid, though it can certainly be very helpful compared to the High School Hell I'm about to dump on him. :-)
Finally, Todd, I did EXACTLY the same thing you are doing right now...I thunk up in my mind a 'tank', and tried to go about building it. I also ran into the same problems you have. Unfortunately, I'm now fixated on solving the general problem of "automated" paper models, versus modelling itself, so I never finished my tank. Alas...
Anyway. For the techno weenies floating about...pull up a slate and some chalk, dig out your abacus, and we'll figger out how to create these shapes for Todd.
The problem is that when you've got an orthographic view of an object, if the panel that you're studying is not parallel to the plane of the view, all of your measurements are distorted. Perspective views make the problem even worse, but they are correctable. We shall not deal with those today. :-)
However, using the different side views of an object, you can pretty easily find out the 3D coordinates of each panel you're interested in. I'm focusing on panels, because a lot of Paper Modeling is the manipulations of the panels.
Granted there are some of those real nasty "puzzle views" that you see on tech. drawing tests where they give you the top and side view of something, and they want you to draw a 3D, isometric view. We're not considering those kind of views either. The model is in your head, mostly, and paper is just a rough manifestation of it.
The problem that Todd ran into is something I bumped into almost immediately, and I specifically designed my tank to have odd angled faces.
So, what to do?
What to do is to find out where your high school math teacher lives, get on your knees and bow down in that general direction while chanting "I should have listened! I should have listened!". That nightmare called "Trigonometry" that everyones drags through in school rears its ugly head for something "real".
Of course, being a geek, I did listen in school, I knew trig was the answer, but all of the details left me. Which, in the long term, is probably worse because the solution was there, but still comepletely evasive.
Now, my friends 70 year old retired aerospace engineer Father knew the answer, but I think anyone who had to design high performance aircraft using stone knives, animal skins, and colored beads during their formative adult years, would probably remember such minutae.
He was an easy reference. Another reference was my 15 year old Algebra II text book that I still kept around. Generally, I find text books fairly useless as they are designed to have a teacher supplement them, and seem to make it difficult to find important information quickly by the student (like the formulas for exams, perhaps...). But I persevered, and managed to figure it out. It was just like riding a bicycle, except I kept falling off the damn thing.
Now, my handy reference that I keep nearby is, of all things, "Cliffs Quick Review - Trigonometry". Cliff notes for math. GREAT book. They also do Physics, and Geometry, and all sorts of things. Ask your favorite bookseller for details.
We'll deal with a generic, 3D triangle that is not parallel with either plane that you've been able to draw. (The techniques work everywhere, of course, but if you just drew it...well...anyway). If the shape you are dealing with is NOT a triangle, then you need to break it up into triangles. If the shape is some kind of conic section (like the Enterprise Hull, but, say just a piece), then you are free to run away screaming into the night, as I'm not dealing with that here. Or, you can choose to make it into a whole bunch of triangles. But, while that may solve the problem, running away into the night is much more satisfying.
Step 1: Determine the lengths of the sides of the triangles.
This is easy. Pythagoreans Theorem conveniently expands from two dimensions into three dimensions. I would imagine it would even work for four dimensions, however this isn't TIME-MACHINE-L, so we'll stop there.
Given two 3D points (x1, y1, z1) and (x2, y2, z2), you can find the length of the line by:
length = sqr((x2-x1)^2 + (y2-y1)^2 + (z2-z1)^2)where sqr() is the square root. Try this at home boys and girls, it works just ducky.We will call the lengths of the triangle A,B, and C. Also, we will assume that A represents the longest of the three lines.
We will also call the angles OPPOSITE the lines a,b, and c respectively.
|\ C |b\ A | \ |a_c\ BPardon the art, but I wanted to get the idea of opposite angles clear.
Step 2: Solve for 'a'.
This is a nice step, because it solves for the largest angle of the triangle, and it is unambiguous. It will reveal immediately whether the triangle is an acute ('a' less than 90 deg.), right ('a' equals 90 deg.), or obtuse ('a' greater than 90 deg.).
To do do this, we will use what is known as "The law of Cosines". The LoC states:
A^2 = B^2 + C^2 - 2BC cos aWhere, as said earlier, A, B, and C are the lengths of the sides of the triangle, and 'a' is the angle opposite 'A'. This relationship holds for all of the angles, not just 'a', but I won't list those.
So, going to the year before Algebra II and using Algebra I, we solve for 'cos a':
B^2 + C^2 - A^2 cos a = ----------------- 2BCOnce we know the cosine of 'a', we can use the what is known as the arccosine, or acos, or cos^-1. Essentially, this is the function that when given a cosine will return the number of degrees that created the cosine.
Filling in the variables, and using the arccosine, we now know what the angle 'a' is for the triangle. One down, two to go.
Step 2: Solve for 'b'
Here, we go to the brother of the LoC into the "Law of Sines". The LoS is represented like this:
sin a sin b sin c A B C ----- = ----- = ----- or ----- = ----- = ----- A B C sin a sin b sin cBasically, the ratio of the triangle leg and the sin of the opposite angle is the same for all of the legs in a triangle. Whoever thought this stuff up was pretty durn crafty.
So, we will use this capability to solve for 'b'.
B sin a sin b = ------- AAgain, we will use the arcsin to find the actual angle for 'b'.
Step 3: Solve for 'c'.
This one is easy. We already know 'a' and 'b'. We also know that all triangles have 180 degrees in them.
Therefore:
180 = a + b + cSo:c = 180 - (a + b)Voila'! QED even!
Now, to jumpstart your heart after dealing with all of that, a few points.
1. Perhaps asking Bob about how to do it using a compass and a ruler would be a better technique :-).
2. If you have a programmable calculator, this math is real easy to do! You don't even have to know much about programming the calculator, as most are really very good at memorizing keystrokes so that you can repeat them over and over, which is what you'd like to do. IMHO, getting this done is your best bet as calculators are disgustingly handy things to have compared to a computer.
3. Finally, here are some formulas for a real simple spreadsheet that you can try. It should work with any spreadsheet program you've got, they're all pretty similiar for such simple math. I'm going to assume you know how to enter a forumala into a spreadsheet cell. We'll use nine cells.
A1 = A (as above - you'll enter these. This is your triangle) A2 = B " A3 = C " B1 = ACOS((A2^2+A3^2-A1^2)/(2*A2*A3)) B2 = ASIN(A2*SIN(B1)/A1) B3 = 3.14159-(B1+B2) C1 = B1*180/3.14159 C2 = B2*180/3.14159 C3 = B3*180/3.14159After you've entered the final side of your triangle, you should have the degrees of the angles in the C column. Remember, these are the opposite angles. For whatever historical reason, scientists and engineers like to deal with Radians, rather than Degrees, so most computer trig functions work with Radians instead of Degrees. The B column is your answer in Radians, but none of my protractors measure these, just Degrees. So, the C column converts from Radians to Degrees for us automagically. Unless you are careful, you may have a similiar problem with your calculator. Many calculators have "modes" that tell it whether to work in Degrees or Radians, so you'll have to check your calculator manual on how to verify these modes.
As a simple test, your spreadhsheet should look something like this:
| A | B | C | +-----+-----------+-----------+ 1 | 5 | 1.570796 | 90.00008 | 2 | 4 | 0.927295 | 53.13015 | 3 | 3 | 0.643498 | 36.86978 |Basically this says that in your everyday 3-4-5 right triangle, this is your solution. Make it a point to round your degrees, its only paper you know.
Sorry all for the length, but I wanted to go into detail about how the problem is solved, as knowing how to solve the problem is usually more valuable than the solution itself.
Also, it would not surprise me that there is a more efficent way (there has to be in fact) of just taking the 3D Plane (a triangle in this case, but generally any 3D plane) and running the plane through a transformation that rotates it onto a plane parallel with one of the axes. The trick is figuring out which angles to rotate the plane by. This is what a programmatic solution would do, and it would work for any polygon, rather than just triangles. But, it also involves mutliplying matrices together and other ugly things.
from Todd Spencer <lildog@inreach.com>: O.k. the first sentence got me! are these points,(x1, y1, z1) and (x2, y2, z2), the visual length or the actual length? hopefully not actual because that is what we are trying to find. How do I arrive at these measurements?
from Will Hartung <vfr750@netcom.com>: Oh, for wish of a greasy table, hot chocolate with whipped cream, a dim flickering yellow candle, and a paper napkin with a pen. You'd get it in a nano-second with such advanced tools. Computers have been designed this way.Instead, we're stuck with e-mail. :-)
_______ |\ /| | | \ / | | 2 Z | X | Y ^ | | / \ | | / \ |/___\| 1/___\3 -X- -X- Top View Side View - not to scale 8-)Assume that everything is square on these...umm..drawings.
On the top view we have shown the X and Z axes, while on the side view we have the X and Y axes.
Let's derive the three points for the front panel (face) of the pyramid. (Numbered on the side view).
Point 1 is easy: x:0, y:0, z:0.
Point 2 is tougher:
From the X-Z chart we see that X marks the spot at x:2 and z:2
From the X-Y chart we see, well, the same thing - x:2 and y:2
(It should be obvious in this case, the X coordinate has to be the same, otherwise it wouldn't be the same point.)
Point 3 is x:4, y:0, z:0.See, while the line segments and angles cannot accurately be measured from the drawing, the end-points CAN be measured, as they are not distorted.
So, the final coordinates for the front face are:
0,0,0 2,2,2 4,0,0To find the length of the first leg (pts. 1 to 2)
sqr((2-0)^2 + (2-0)^2 + (2-0)^2) = sqr(2^2 + 2^2 + 2^2) = sqr(4 + 4 + 4) = sqr(12) = 3.46The first leg is the same as the second leg, in this case. Let's find the third (pts 3 to 1):
sqr((4-0)^2 + (0-0)^2 + (0-0)^2) = sqr(4^2) = 4Of course, we could have measured the base, but at least the math still works (always encouraging).
So, your triangle has sides of 3.46, 3.46, 4.
Plugged into the spreadsheet, and you get the angles: 54.6, 54.6 and 70.6. Fudge for rounding to 55, 55, and 70 (notice that it's not 55,55,71 as the degrees have to add up to 180).
There is a lot of symetry in models, so take advantage of it. No need to calculate the same numbers twice. Plus, once you know the length of a leg, you can use it for the shared panels, etc.
The hot tip is to draw your views, then start filling in the blanks for the angles and lengths. Take advantage of parts that are the same on both sides of a model, but perhaps flipped over.
from Todd Spencer <lildog@inreach.com>: One point... once you get the length of a sides you don't need the angles because there is only one way the sides will fit together with the given lengths. Right?
from Will Hartung <vfr750@netcom.com>: Well, yes and know. Obviously a triangle defined by SSS (side, side, side) is defined and unique. Whereas there are an infinite number of triangles expressed as AAA.But, that's geometry. You're trying to actually draw these things out. If I wanted to draw an SSS triangle, I'd be hard pressed to get it right the first time with just a pencil and ruler. You really need to know SAS to draw an accurate triangle with a ruler and a protractor, and get it right the first time. [Editor's note: actually, with a straightedge and compass or dividers, it's pretty easy to draw the SSS triangle, and this is probably more accurate than trying to do it with a protractor.]
Once you've got those first two legs drawn, the third is a simple closure of the triangle. But you knew that.
from Todd Spencer <lildog@inreach.com>: I would like to try my hand at designing a model and have a few questions for you more experienced modelers out there. I would like to try to build a simple model of the Enterprise from Star Trek. My one big question is how do you go about making a saucer shape from paper? I need two pieces that are shaped like paper plates, only much smaller. Is this possible? I think they call this a compound curve, right?
from Steve Brown <cardfaq@bellsouth.net>: First, on the question, is it a compound curve? I don't know, because I'm not familiar with that term in this context. Strictly, curves are one-dimensional; the corresponding two-dimensional object is called a surface. Surfaces can be classified as not curved (i.e. planar), singly curved, and doubly curved (which may be what you mean by compound surface). Not curved is, I hope, obvious.Singly curved means that the surface can be mapped to a plane without stretching or compressing. A property of singly curved surfaces is that the intersection of the surface and the tangent plane at any point is a line. The curve which is normal to all of these lines is called the 'line of stretchout' or 'arc of stretchout', a concept which is easy to explain with diagrams and a few examples, but is otherwise very difficult to describe. It's the line or curve on which the surface will 'unroll'. Examples of singly curved surfaces are cylinders and cones.
Doubly curved means that the surface cannot be mapped to a plane without stretching or compressing. The canonical example is a sphere--you can't press an orange peel flat without tearing it (this is also why Greenland looks so big on many maps.) A property of doubly curved surfaces is that the intersection of the surface and the tangent plane at any point is a point. Paper models necessarily approximate doubly-curved surfaces as sets of singly-curved ones.
For the Enterprise saucer, the prototype is probably doubly curved, but it's closely approximated by a set of singly curved surfaces. As I recall, it's a disk, with frustrums of cones set on top and bottom, and a little hemisphere on top. The hemisphere is challenging, but the rest is straightforward.
Some vocabulary: A frustrum of a cone is a cone with the pointy bit chopped off. An annulus is a disk with the center cut out (like a washer.)
Now for the equations.
I'll assume you can handle a right circular cylinder alright. To form a right circular cone of height h and base diameter D, you need a flat piece shaped like a pie serving. The radius of the 'pie' is
R = sqrt[ h^2 + (D/2)^2 ]and the included angle ispi * D / R (in radians)To form a frustrum of a right circular cone, you need a shape like a pie piece with the tip removed. For a frustrum of height h, with the top diameter d and the base diameter D, you need a section of an annulus with the outer diameter
R = D * sqrt[ h^2/(D-d)^2 + 1/4 ]and the inner diameterr = d * sqrt[ h^2/(D-d)^2 + 1/4 ]and the included angle is againpi * D / R = pi * d / r (in radians)Things get more complicated for other shapes. Right circular cylinders with one face canted are fairly straightforward, but non-circular cylinders or frustrums with canted faces involve more than just trigonometry. Also, any of this is hard to explain without pictures (I'm afraid that what's above may already be unclear without diagrams.)
Spheres and domes are also complicated, because they are doubly curved shapes and must be approximated by singly curved surfaces.
from Timothy A. Good <timgood@snip.net>: Frustum of cone (a.k.a. lampshade) is ((r/s) * 360) where r=3D radius of the base, s=3D true slant height of the cone (length of the sloping sides from base to where they intersect if it was a true pointy cone). Result is the included angle of the flat drawing. My mom did a lot of lampshades using this formula, tracing out designs of flowers and leaves etc. doing partial cuts and curling sections for a neat effect.
from Bob Bell <bobbell@portal.connect.ab.ca>: When I make domes I cheat. The first method I use is to find a similar dome in another kit then scan it into my Coreldraw programme and reduce or enlarge it to the size I want. The second "cheat" (for a clear dome such as a bubble gun turret on the Lancaster bomber) I found that clear plastic chocolate moulds, available in craft stores, come in all szes and shapes, some of which make perfect domes. To actually design a dome, which I have to do for some of my locomotives, I make it in three parts. The bottom is a cylinder, the second is a truncated cone, and the third is a flat circle.
from Emil Zarkov <modelart@tusk.icn.bg>: Whatever the paper modeler does, he must approximate the double concave surfaces with surfaces that are capable of being formed without elastic deformation, i.e. flat or with single concavity.
There are at least four ways to represent the sphere.
1. If you chose flat surfaces for approximation, you may start from tetrahedron, cube, octahedron, etc. and increasing the number of flat polygons, you may achieve something that approximates a sphere very well. Remember the mirror balls in the discotheques.
If you use single concave surfaces you have at least 3 other choices. For two of them there is an explanation from Mr. Kell Black:
2. The zone method.
3. The gore method.
These two methods are the most popular in the card modeling, because of the easy calculation of the theoretical shapes of the segments.
Now is my turn.
4. You can make a spheroidal surface, using only one spiral segment. Please realize what happens when you peel an apple. You have spheroidal surface at the beginning and you transform it to flat surface when you finish. Now imagine that you bend the peel into its initial shape. Thus you can make not only the sphere, but also the whole spacecraft from one very, very long part. Terrible, but possible. [Editor's note: an example of Dr. Zarkov's single piece sphere design is available from Moshe Lemer's web site.]
from Jeff Tupper / Pedagoguery Software Inc <tupper@peda.com>: Geodesic domes can be used to approximate hemispheres; geodesic spheres can be used to approximate spheres. Both can be made from paper (all of the faces or polygons).
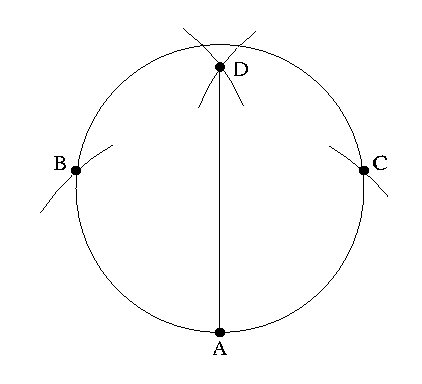 Here is a classical (i.e. compass and straight edge) method of finding the
center of a circle:
Designate a point A on the edge of the circle. Strike an arc from
that point to define the points B and C on the circle
equidistant from A. You now wish to bisect the chord BC.
From B, strike an arc, and from C, strike another arc of
the same radius. The intersection of the two arcs defines the point D.
The line AD passes through the center of the circle.
Here is a classical (i.e. compass and straight edge) method of finding the
center of a circle:
Designate a point A on the edge of the circle. Strike an arc from
that point to define the points B and C on the circle
equidistant from A. You now wish to bisect the chord BC.
From B, strike an arc, and from C, strike another arc of
the same radius. The intersection of the two arcs defines the point D.
The line AD passes through the center of the circle.
Now designate another point on the circle, and repeat the process. The intersection of the two lines is the center of the circle.
If you know the radius of the circle, set a compass to that radius and strike an arc centered on the edge of the circle. The arc will pass through the center of the circle. Repeat this from a different point on the edge of the circle, and the two arcs will intersect at the center.
A quicker method is to use a center-finder, but if you don't have one,
the compass and straight-edge are sufficient.
from Robin Day <rday@pangea.ca>: Anyone know of a method to determine the length of a curved line without having/knowing the diameters of the arcs? I would be interested in methods involving geometry formulae, Macromedia FreeHand, or Adobe Illustrator. I know most CAD software allows for measuring almost anything, but I do not have access to this type of software. I would prefer formulae if anyone has some insight.
from Todd Anderson <bigtodd@vnet.net>:
from robin day <rday@pangea.ca>: FreeHand uses Bezier curves for all of its splines and does give cartesian coordinates for the curve handles. Would you happen to know if this information can be used to resolve the curve? Unfortuantely, I don't know what kind of geometry drives Bezier based curves.
from Steve Brown <cardfaq@bellsouth.net>: Now you're getting specific. The Bezier curve is a cubic polynomialR(u) = (1-u)^3 R0 + 3u(1-u)^2 R1 + 3u^2(1-u) R2 + u^3 R3where R0, R1, R2, R3 are the defining points and 0<=u<=1.(It can be generalized to orders other than 3 as the Bernstein-Bezier [sic] curves, and further generalized into something called B-splines, which I've never really tried to study. But the Bezier curve itself has that nice polynomial form. When several Bezier curves are concatenated into a spline, they may enforce additional constraints of continuity of the derivatives at the joining points, which may screw up all that follows.)
Note that, although it's written as a bivariate polynomial (in u and 1-u) it's really just a cubic. The squared norm of the incremental length (chord) actually has a nice closed form expression in terms of the vertices of the defining polygon. Let
P1 = R1 - R0 P2 = R2 - R1 P3 = R3 - R2anddR/du = 3(1-u)^2 P1 + 6u(1-u) P2 + 3u^2 P3All we actually need are the inner products:T11 = <P1,P1> = |P1|^2 T12 = <P1,P2> T13 = <P1,P3> T22 = <P2,P2> = |P2|^2 T23 = <P2,P3> T33 = <P3,P3> = |P3|^2and then the squared chord isS(u) = |dR/du|^2 = A^2 T11 + B^2 T22 + C^2 T33 + 2AB T12 + 2AC T13 + 2BC T23whereA = 3(1-u)^2 B = 6u(1-u) C = 3u^2and the arc length is thusL = integral(0 to 1) sqrt[S(u)] duand this is as far as I've gotten. Note that despite the messy notation, S(u) is just a 4th order polynomial and it may be possible to do a closed form evaluation of the integral. But my bag o' tricks for integration is pretty dusty, and no clever factorizations of S(u) have occurred to me, except for some special cases.That dependence only on the lengths and angles of the defining polygon is really elegant, confirming that the length of the curve is invariant under translation. I always get a kick out of it when a lot of grungy math ends up proving something really self-evident.
I confess that if I needed an answer to this tomorrow, I'd implement a numerical solution. I'm pretty sure, but haven't proved, that L is nice and smooth in all the important senses, and a numerical integration should converge nicely. A third order interpolation would probably converge very fast, but Simpson's Rule would probably be fast enough for reasonable precision.
Note that I think that there is no choice of R0-R3 for which the Bezier curve is a circular arc.
cardfaq@bellsouth.net
| Steve Brown
|